Occupation number generating function

Master equations are simply system of differential equations and can therefore be solved by the usual techniques. When looking for a steady-state solution, we can simply set all time derivatives to zero and try to solve for the occupation numbers at equilibrium. These system often contain a large or even infinite number of equations, but for most model their structure should be regular. This allows us to write recursion formula for the equilibrium values. Recursion that, if lucky or creative enough, we could solve explicitly. Or we could be a bit more systematic and attempt this approach using probability generating functions.

Consider the following generating function,

\[ G(x,t) = \sum _{n=-\infty}^{\infty}P_n(t)x^n \]

which is defined over all integer values of \(n\). \(G(x,t)\) is a probability generating functions since its coefficients \(P_n(t)\) are occupation numbers, and therefore positive coefficients, such that \(G(1,t) = 1\) for all time \(t\).

Interestingly, the Method of Moments is now neatly rewritten as derivatives of \(G(x,t)\). For example, we can write

\[ \langle n(t)\rangle = \sum_{n=-\infty}^{\infty} nP_n(t) = \frac{\partial G(x,t)}{\partial x}\bigg\vert_{x=1} \; , \]

and

\[ \langle n(t)^2\rangle = \sum_{n=-\infty}^{\infty} n^2P_n(t) = \frac{\partial}{\partial x}\left(x\frac{\partial G(x,t)}{\partial x}\right)\bigg\vert_{x=1} \; . \]

More generally, our goal can now be to rewrite master equations (large systems of differential equations) in terms of a single partial differential equation for \(G(x,t\)). While these might not be easier to handle numerically, they can sometimes be solved directly. This happens rarely to be honest, but we give a few examples of techniques to try.

Equilibrium of the linear birth-death process

Consider the birth–death process with a fixed constant birth rate \(\mu\) for particles and a fixed death rate \(\nu\) for all active particles. This is a system we also tackle with numerical integration, which means we know it contains a steady-state distribution over all occupation numbers. For this process, our master equations are defined as follows for \(n\geq 0\),

\[\begin{split} \begin{align} \frac{d}{dt}P_n(t) &= -\mu P_n(t) + (n+1)\nu P_{n+1}(t) \quad \textrm{for n=0}\\ \frac{d}{dt}P_n(t) &= -(\mu + n\nu)P_n(t) + (n+1)\nu P_{n+1}(t) + \mu P_{n-1}(t) \quad \textrm{for n>0}\\ \end{align} \end{split}\]

Equivalently, we can use a equation for all \(n\) and simply state that \(P_{n<0}(t) = 0\):

\[ \frac{d}{dt}P_n(t) = -(\mu + n\nu)P_n(t) + (n+1)\nu P_{n+1}(t) + \mu P_{n-1}(t) \]

The method of generatingfunctionology [Wilf, 2005] is to multiply both sides of such an equation by \(x^n\) and sum over all values of \(n\). This gives us

\[\begin{split} \begin{align} \sum_{n=-\infty}^{\infty} \frac{d}{dt}P_n(t) x^n &= \sum _{n=-\infty}^{\infty} \left[-\mu P_n(t)x^n - n\nu P_n(t)x^n + (n+1)\nu P_{n+1}(t)x^n + \mu P_{n-1}(t)x^n\right] \\ \frac{\partial}{\partial t} G(x,t) & = -\mu G(x,t) - x\nu\frac{\partial}{\partial x}G(x,t) + \nu\frac{\partial}{\partial x}G(x,t) + x\mu G(x,t) \\ \frac{\partial}{\partial t} G(x,t) & = (1-x)\left[\nu \frac{\partial}{\partial x}G(x,t) -\mu G(x,t)\right] \end{align} \end{split}\]

In some cases, partial differential equations of this type can be solved explicitly using the method of the characteristics. In practice however, we tend to use this approach to solve for the steady-state value \(G(x) = \lim_{t\rightarrow\infty} G(x,t)\) where we assume that the temporal derivative of \(G(x,t)\) is equal to zero. We therefore have

\[\begin{split} \begin{align} 0 &= (1-x)\left[\nu\frac{d}{dx}G(x) - \mu G(x)\right] \\ \frac{d}{dx}G(x) &= \frac{\mu}{\nu}G(x) \end{align} \end{split}\]

This is a simple case where, recalling our lovely calculus courses, we get

\[ G(x) = \exp\left(\frac{\mu}{\nu}x + C\right) \]

where the constant of integration can be identified through our normalization condition \(G(1) = 1\) such that

\[ G(x) = \exp\left(\frac{\mu}{\nu}(x-1)\right) \]

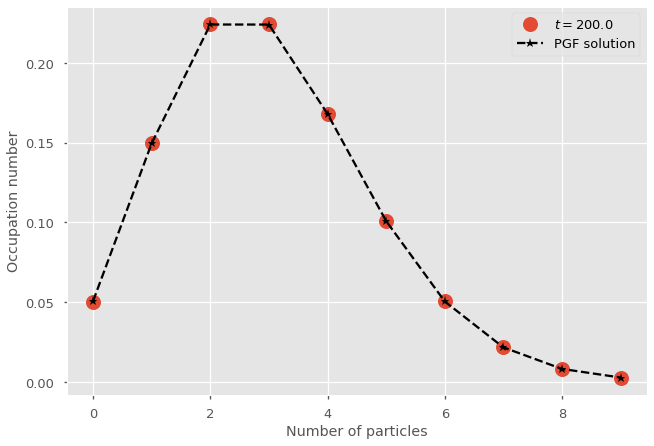
Comparison with numerical integration

import numpy as np
import matplotlib.pyplot as plt
plt.style.use(['ggplot', 'seaborn-talk'])

# We will use the odeint routine
from scipy.integrate import odeint

# Master Equations
def J(x, t, mu, nu):    
    dx = 0*x
    for n in range(len(x)):
        if n==0: #for first state
            dx[0] = - mu*x[0] + nu*x[1]
        elif n==len(x)-1: #for last state
            dx[n] = -(nu*n)*x[n] + mu*x[n-1]
        else: #all other states
            dx[n] = -(mu+nu*n)*x[n] + nu*(n+1)*x[n+1] + mu*x[n-1]

    return dx

# Time of observations
t_length = 200
t_steps = 10
t_vec = np.linspace(0, t_length, t_steps)

# Initial conditions
nb_of_states = 10
x_0 = np.zeros(nb_of_states)
x_0[0] = 1

# Parameters
mu = 0.3
nu = 0.1

# Numerical integration
G = lambda x, t: J(x, t, mu, nu)
x_path = odeint(G, x_0, t_vec)

# PGF solution
G = lambda x: np.exp((mu/nu)*(x-1))
G = np.vectorize(G)
N = nb_of_states
n = np.arange(N)
c = np.exp(2*np.pi*1j*n/N)
pn = abs(np.fft.fft(G(c))/N)

# Plot
plt.plot(range(nb_of_states),x_path[-1], marker="o", lw=0, ms=15, label=fr"$t = {t_vec[-1]}$")
plt.plot(range(nb_of_states),pn, marker="*", ls='--', color='k',label=r'PGF solution')
plt.legend()
plt.ylabel('Occupation number')
plt.xlabel('Number of particles')
plt.show()

General solution to an exponential birth-death process

Consider now a birth-death process representing cell division. Active cells divide at rate \(\mu\) and die at rate \(\nu\). For this process, our master equations are defined as follows for a number of active cells \(n\geq 0\),

\[\begin{split} \begin{align} \frac{d}{dt}P_n(t) &= -(\mu + \nu)nP_n(t) + (n+1)\nu P_{n+1}(t) \quad \textrm{for n=0}\\ \frac{d}{dt}P_n(t) &= -(\mu + \nu)nP_n(t) + (n+1)\nu P_{n+1}(t) + \mu (n-1) P_{n-1}(t) \quad \textrm{for n>0}\\ \end{align} \end{split}\]

This process has an absorbing state at \(n=0\), such that we do not expect a steady-state solution as in the previous model with linear birth. Instead, we are more likely to be interested in the extinction probability of the process:

\[ P_{\textrm{ext}}(t) = P_0(t)=G(0,t) \; . \]

We can attempt to solve this probability with a direct solution of the system. We use the same recipe as in our previous example to reduce our set of infinitely many coupled master equations to a single partial differential equation. In this case, we should obtain

\[ \frac{\partial}{\partial t}G(x,t) = \nu(1-x)\left(1-\frac{\mu}{\nu}x\right)\frac{\partial}{\partial x}G(x,t) \; . \]

Since we do not expect a steady-state solution, we cannot ignore the left-hand side of the equation and must attempt a time-explicit solution. We use the Method of characteristics where the idea is to look for a solution as a characteristc curve (or line) in \(x(s)\) and \(t(s)\) space that depends on a single characteristic curve parameter \(s\)along which \(dG/ds = 0\). If such a solution exist, it must follow the total derivative rule such that

\[ \frac{d}{ds} G\left(x(s),t(s)\right) = 0 = \frac{\partial G(x,t)}{\partial x}\frac{dx(s)}{d s} + \frac{\partial G(x,t)}{\partial t} \frac{dt}{ds} \; . \]

Along this characteristic curve in \(s\), we would then simply have a constant function where dependencies in \(s\) balance out. That’s by definition, such that we are looking for a solution under strong assumptions which is why the method does not always work. When it does, the behaviour of \(G(x,t)\) is then fully contained within our initial conditions (\(x(0)\) and \(t(0)\)) as well as the shape of \(x(s)\) and \(t(s)\). In our case that’s

\[ G\left(x(s),t(s)\right) = G\left(x(0)=x_0,t(0)=0\right) = x_0^{n_0} \; . \]

To find such a function, we can set \(t(s) = s\) such that the last term of the null total derivative condition gives us the left-hand side of the partial differential equation of our model. Equating the two, we are then left with a single ordinary differential equation to solve:

\[ \frac{dx(s)}{ds} = \frac{dx(t)}{dt} = -\nu \left[1-x(t)\right] \left[1-\frac{\mu}{\nu}x(t)\right] \rightarrow -\nu dt = \frac{dx}{\left[1-x(t)\right] \left[1-\frac{\mu}{\nu}x(t)\right]} \]

Integrating on both side from \(x_0\) to \(x\) (assuming \(\mu \neq \nu\)) and solving for \(x_0\), one can then find the time-explicit solution to this model.

\[ G(x,t) = \left[\frac{(\nu-\mu x)e^{(\nu-\mu)t}-\nu(1-x)}{(\nu-\mu x)e^{(\nu-\mu)t}-\mu(1-x)}\right]^{n_0} \]

With this general solution, we can explicitly write the extinction probability as a function of time,

\[ P_{\textrm{ext}}(t) = P_0(t)=G(0,t) = \left[\frac{\nu e^{(\nu-\mu)t}-\nu}{\nu e^{(\nu-\mu)t}-\mu}\right]^{n_0} \; . \]

With this expression, we can recover a known result from our branching process studies. In the large time limit, \(t\rightarrow \infty\), we find

\[ P_{\textrm{ext}} = \lim_{t\rightarrow \infty}P_0(t) = 1-\left(\frac{\nu}{\mu}\right)^{n_0} \; . \]