Detailed balance

We started the previous section by stating the obvious: Master equations are simply systems of differential equations and can therefore be solved by the usual techniques. However, there are many additional restrictions to master equations that allow us to define useful tools for their analysis. In particular, master equations track occupation numbers which represent a probability mass function. Therefore, the variables of this system of equations are always positive and must sum to one.

The steady states of master equations sometimes follow a highly constrained set of flows that can help solve the exact equilibrium values. We say that a system follows detailed balance when the input and output flows between each pairs of states balance each other (i.e., every transition is reversible and used as frequently in each direction). Mathematically, we can write

\[ J_{n\rightarrow m} = J_{m\rightarrow n} \quad or \quad \omega(n,m)P_n = \omega(m,n)P_m \quad \forall \; n,m \]

where the second equality highlights how this equality between flow of probability mass can be expressed as an equality between rates of transition \(\omega\) and occupation numbers \(P_n\) for all pairs of states. It follows that, in a system following detailed balance, the ratio of occupation numbers at steady state can be written as

\[ \frac{P_m}{P_n} = \frac{\omega(m,n)}{\omega(n,m)} \]

which is a very restrictive condition and can make exact solution at equilibrium much easier.

Solution to the birth-death process

We have been using a simple birth–death process as an example for a while now. Our previous, explicit, solution used the full master equation,

\[\begin{split} \begin{align} \frac{d}{dt}P_n(t) &= -\mu P_n(t) + (n+1)\nu P_{n+1}(t) \quad \textrm{for n=0}\\ \frac{d}{dt}P_n(t) &= -(\mu + n\nu)P_n(t) + (n+1)\nu P_{n+1}(t) + \mu P_{n-1}(t) \quad \textrm{for n>0}\\ \end{align} \end{split}\]

However, instead of asking all flows to equal zero on every cell, we can instead ask flows in both direction to match for each transition. This gives us a much simpler recursion than in the previous section. Namely, using detailed balance, we write

\[ \frac{P_n}{P_{n-1}} = \frac{\mu}{n\nu} \; . \]

Let \(P_0\) be its own thing to start the series. One can then write the next few terms as \(P_1 = \frac{\mu}{\nu}P_0\), \(P_2 = \frac{\mu^2}{2\nu^2}P_0\), and quickly generalize to

\[ P_n = \frac{1}{n!}\left(\frac{\mu}{\nu}\right)^n P_0 \; . \]

And all that is left is to solve for \(P_0\). What else can we use? Our normalization condition: \(\sum_n P_n = 1\). We therefore write

\[ \frac{1}{P_0} = \sum_{n=0}^\infty \frac{1}{n!}\left(\frac{\mu}{\nu}\right)^n = e^{\mu/\nu} \]

where we used the Taylor series of the exponential function to simplify the sum and get the last equality.

We relatively easily re-obtained our previous solution using the principle of detailed balance:

\[ P_n = \frac{1}{n!}\left(\frac{\mu}{\nu}\right)^n e^{-\mu/\nu} \; . \]

Defining equilibrium through detailed balance

Let us now do a simple experiment using detailed balance in a system at equilibrium in an unspecified number of dimensions. We start this step at state \(n=0\), which is nothing special, and first move to state \(n=1\). The occupation number at that state is therefore \(P_1 = P_0 \frac{\omega(1,0)}{\omega(0,1)}\). Now assume that we do a much longer chain taking us from state 0 to state \(m\), the same logic gives us:

\[ P_m = P_0 \prod _{j=0}^{m-1} \frac{\omega(j+1,j)}{\omega(j,j+1)} \; . \]

If we pause for a second, we can realize that this is the logic we used to solve the previous system using a chain of length one. This was all we needed to account for all mechanisms. However, sometimes, using longer chains can be useful! In any way, the value of \(P_0\) is eventually determined by the normalization condition as we did above.

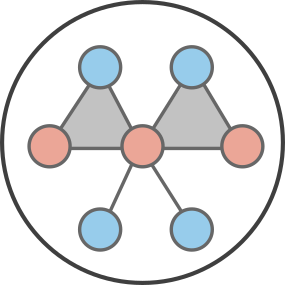
Now, let us close the chain into a loop. Let’s assume that the final state is the first state; i.e., \(m\equiv 0\). Then, the product in our previous expression has to be equal to 1 for \(P_0 = P_0\). This means that over any close loop or cycle \(\Gamma\) in the transition network, we have (if detailed balance holds):

\[ \prod _{j\in\Gamma} \frac{\omega(j+1,j)}{\omega(j,j+1)} = 1 \; . \]

This is an important result as it is independent of any unknown stationary occupation numbers \(P_n\). It simply relates the concept of detailed balance to the mechanistic transitions and their parameters. It can be used to prove that detailed balance holds as a function of the transition rates.